Information on research by Burak Aksoylu

 

Research interests

I work in the areas of numerical analysis, scientific computing, and numerical linear algebra. My research interests include:

  • Nonlocal problems, peridynamics, local boundary conditions for nonlocal problems, preconditioning for peridynamics, scalable solvers for nonlocal problems,
  • preconditioning, iterative solvers, numerical solutions to partial differential equations,
  • multilevel preconditioning, multigrid, preconditioning under adaptive mesh refinement,
  • robust preconditioning for high-contrast heterogeneous media,
  • Krylov subspace solvers.

Research application areas

My research has been used to solve modeling and simulation problems in the application areas that include:

  • Biophysics,
  • Computer graphics,
  • Geosciences,
  • Numerical relativity,
  • Solid mechanics.

Overview

My research concentrates on rigorous numerical methods for solving nonlocal problems and partial differential equations (PDEs) with emphasis on preconditioning. The design, construction, analysis, and implementation of numerical methods that are optimal, robust, and scalable are at the heart my research. These features are critically needed in practically any field because even in modern day simulations, preconditioners and solvers usually take more than half the computational time and storage. I am interested in the supporting mathematical and algorithmic tools from numerical analysis, scientific computing, and numerical linear algebra. More recently, I study in the area of nonlocal wave propagation utilizing tools from operator theory and computational methods to solve the related integral equations.

1 Nonlocal problems

Fig. Wave separation in the classical (left) and nonlocal (right) wave equation.

There are noteworthy developments in the area of nonlocal modeling. For instance, crack propagation and viscoelastic damping are modeled by peridynamics (PD) and fractional derivatives, respectively, both of which are nonlocal. Similar classes of operators are used in numerous applications such as nonlocal diffusion, population models, image processing, particle systems, phase transition, and coagulation. We study instances of successful modeling by nonlocal theories of phenomena that cannot be captured by local theories. PD is a nonlocal extension of continuum mechanics and is capable of quantitatively predicting the dynamics of propagating cracks, including bifurcation. Its effectiveness has been established in sophisticated applications such as successful description of results of Kalthoff-Winkler experiments of the fracture of a steel plate with notches, fracture and failure of composites, nanofiber networks, and polycrystal fracture.

1.1 Incorporating local boundary conditions into nonlocal problems

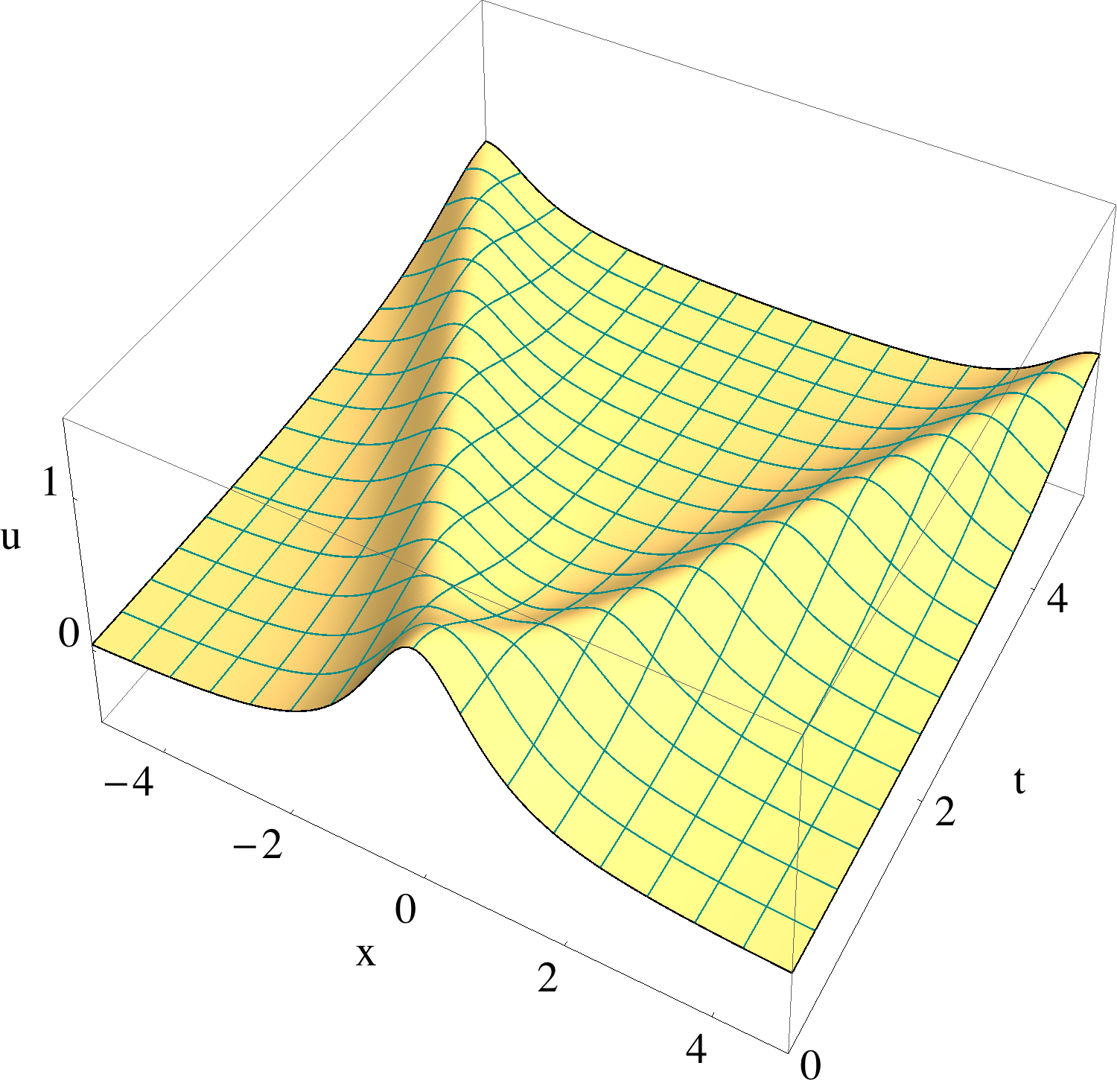
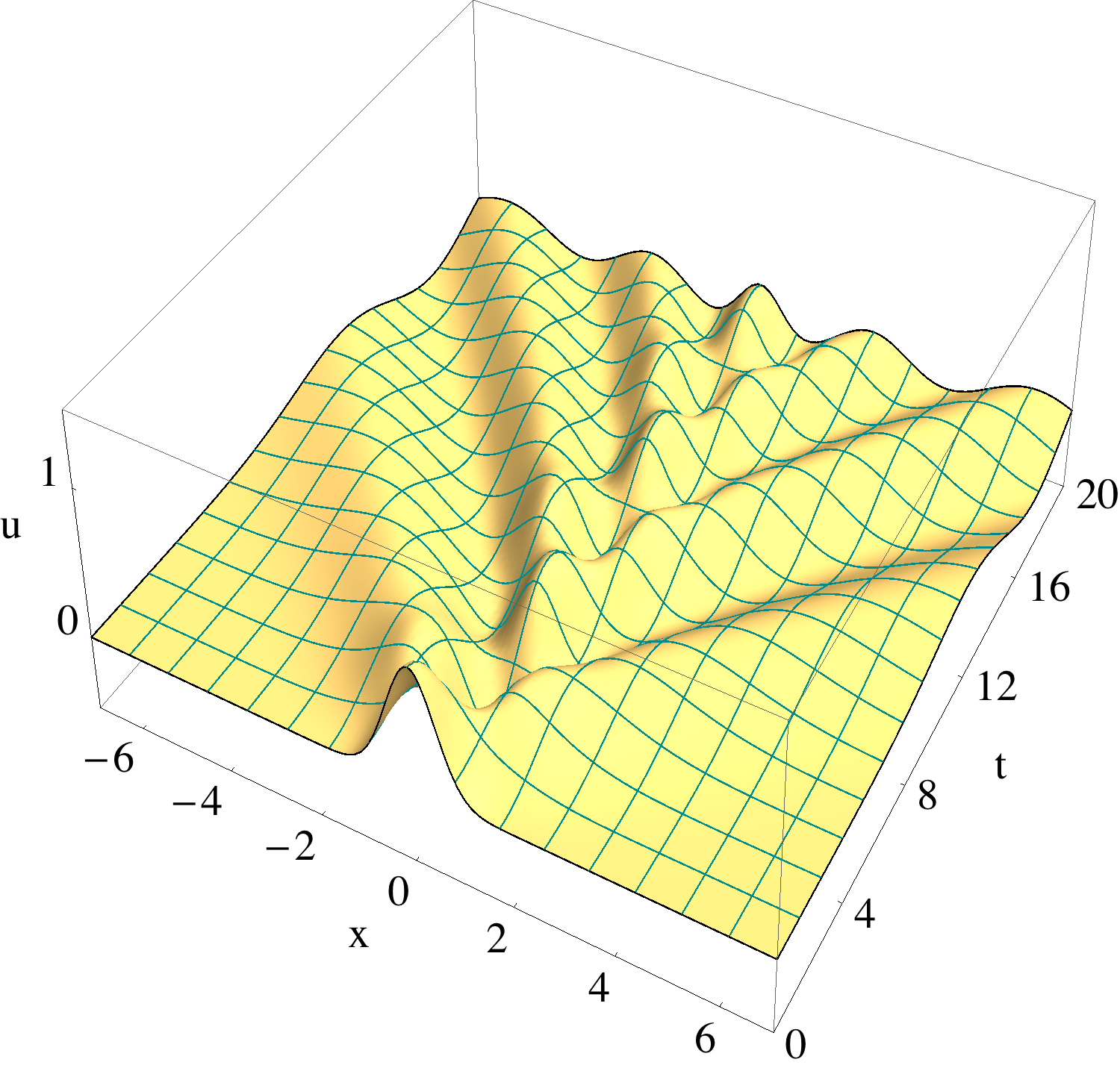
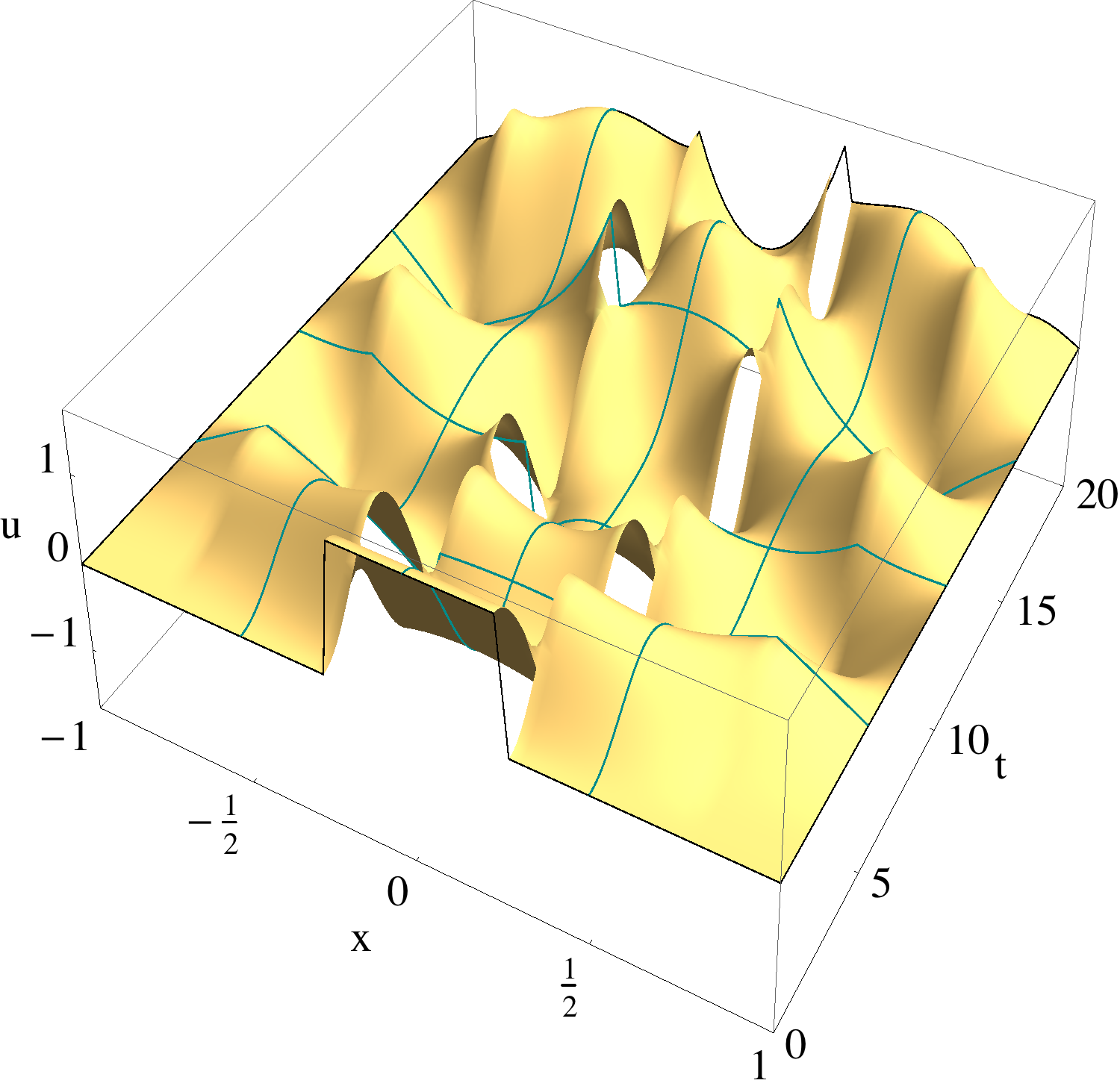
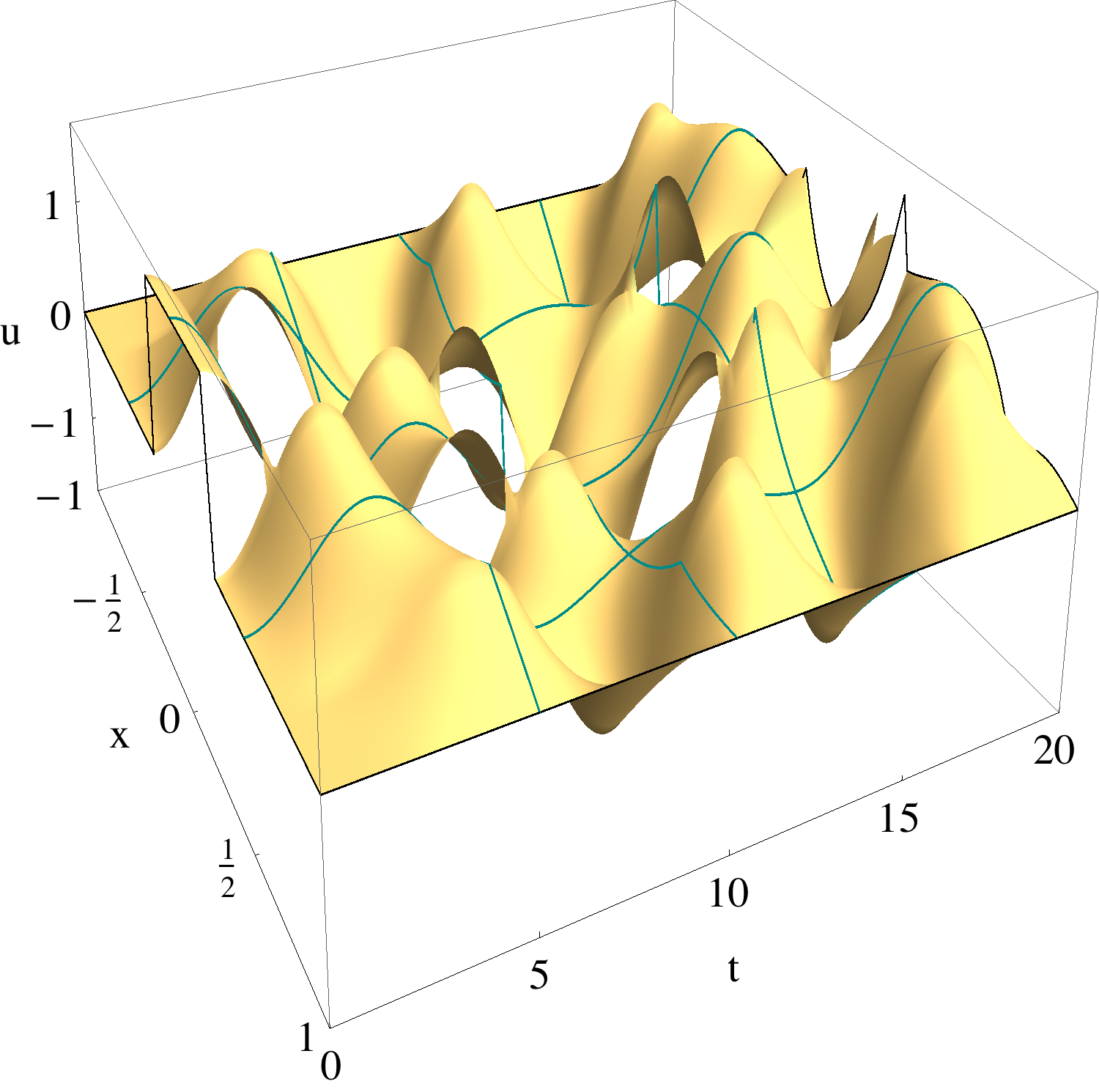
Fig. For all time, local homogeneous Dirichlet boundary conditions are satisfied and discontinuities remain stationary.

Considering wave phenomena only partially successfully described by a classical wave equation, it seems reasonable to expect that a more successful model can be obtained by employing the functional calculus of self-adjoint operators, i.e., by replacing the classical governing operator A by a suitable function f(A). Since classical boundary conditions (BCs) is an integral part of the classical operator, these BCs are automatically inherited by f(A). In this way, we vision to model wave phenomena by using appropriate f(A) and, as a consequence, need to study the effect of f(A) on the solutions. One advantage of our approach is that every symmetry that commutes with A also commutes with f(A). As a result, required invariance with respect to classical symmetries such as translation, rotation and so forth is preserved.

One of our major results is the finding that, in ℝn, the governing operator of PD equation is a function of the governing operator of classical elasticity. This result opened the path to the solution of a long standing and major open problem of peridynamics, namely, the introduction of local boundary conditions into the theory. We solve this problem and eliminate the ``dreaded'' boundary effects seen in PD. The approach is not limited to PD, the abstractness of the theoretical methods used allows generalization to other nonlocal theories. Our approach presents a unique way of combining the powers of abstract operator theory with numerical computing. We complement our approach with comprehensive numerical treatment.

Related publications

1.2 Variational theory and domain decomposition for nonlocal problems

Fig. A domain with its nonlocal (volumetric) boundary (left). A nonoverlapping two-subdomain decomposition (right).

In AkMe2010, we establish a variational framework to study well-posedness of governing equations based on nonlocal diffusion. We utilize a weak formulation of the underlying problem. We give nonlocal Poincaré type inequalities that reveal the horizon δ (the size of nonlocal interaction) quantification. This spectral equivalence with explicit δ-quantification leads to a mesh size independent upper bound for the condition number of an underlying discretized operator:

λK ≤ a(u,u) ⁄ ∥u∥2L2(Ω) ≤ λK,
κ(K) ≲ δ-2

Later, in [AkUn2014], we investigate the sharpness of this δ-quantification.

In [AkPa2011], we give the first domain decomposition study for nonlocal problems. We extend iterative substructuring methods to nonlocal settings and characterize the impact of nonlocality upon the scalability of these methods by characterizing the conditioning of the resulting Schur complement. Furthermore, we introduce a nonlocal two-domain variational formulation utilizing nonlocal transmission conditions, and prove equivalence with the single-domain formulation, a first step in establishing rigorous theory for nonlocal domain decomposition methods.

Related publications

1.3 Sharp condition number bounds for nonlocal operators

In [AkUn2014], we solve a challenging open problem: What is the sharp quantification of the condition number of the involved operators with respect to the underlying parameters? When we study the existing quantifications, we realize that they are not sharp. We use two types of micromodulus functions; singular and integrable. Singular kernels lead to fractional Sobolev spaces Hs(Ω), s ∈ (0,1), to which jump discontinuities belong.

The following spectral bounds we obtain, respectively, provide sharp δ-, h-, and s-quantifications of the extremal eigenvalues for the underlying (both for piecewise linear and piecewise constant finite element) discretizations:

ch ≤ λa ≤ c (5h δ-2 - 6 h2 δ-3)
ch ≤ λb ≤ c (8(21-2s - 1) ⁄ s(1-2s)(3-2s) h1-2s δ-(2-2s) - 8(1-s) ⁄ (3s) h δ-2).

Our results indicate that there are two terms involved in the quantification of the maximal eigenvalue: one positive and one negative. We discover that the available quantifications in the literature are able to recover only the positive term. Hence, what makes our quantifications sharp was the discovery of the negative term. We are even able to find the asymptotic value of c by using Toeplitz matrix techniques; c → π2 as

Related publications

2. Robust preconditioning for high-contrast media

Fig. Diffusion equation solution becomes constant over high-contrast regions.

For elliptic PDEs with high-contrast coefficients, we construct preconditioners that are as algebraic as possible in order to accommodate underlying complex geometry such as reservoirs. Algebraic multigrid (AMG) preconditioner is known to work well for similar class of problems that involve high-contrasts. However, there is no rigorous proof why AMG treats such problems well. We aim to construct rigorously justified algebraic preconditioners that are robust simultaneously with respect to mesh and contrast size.

First, we establish the contrast size robustness in [AkKl2009] [AkKl2007] High contrasts are commonly found in applications, for instance, in reservoir simulations the contrast can be of size O(1018). We study diffusion, biharmonic, and Stokes equations with high-contrast coefficients. We achieve a desirable preconditioning design goal; the same family of preconditioners can be used for different PDEs with varying discretizations. For diffusion equation, linear finite element [AkGrKlSc2008] and finite volume [AkYe2010] discretizations and for biharmonic plate equation, HCT discretization [AkYe2011], and for Stokes equation [AkUn2013], [AkUn2014_stokes], Q2-Q1 (Taylor-Hood element) and stabilized Q1-Q1 finite elements are used. The same family can be extended to high-contrast PDEs of order 2k, k>2. We utilize singular perturbation analysis (SPA) to analyze the limiting behaviours of the underlying discretizations such as low-rank perturbations and the rate of convergence.

The broadness of the applicability of our preconditioner has been achieved by SPA as it provides valuable insight into qualitative nature of the underlying PDE. We can fully reveal the asymptotic behaviour of the solution over the high-contrast regions. This information leads to a characterization of the limit of the underlying discretized inverse operator. We prove that the solution over the high-contrast island converges to a linear and constant polynomial in the case of biharmonic and diffusion equations, respectively. In general, for PDEs of order 2k, k ≥ 1, the solution over the high-contrast islands approaches a polynomial of degree k-1. By this result, we reveal fundamental qualitative features of the solutions of the high-contrast elliptic PDEs. The exploitation of these qualitative features yield the superior performance of our preconditioners.

Related publications

3. Rigorous treatment of diffusion equation with rough coefficients

The study of heterogeneity and its impact on the numerical solution of PDEs heavily relies on structural understanding of the qualitative nature of the underlying PDE operators and their dependence on the coefficients. Our study [AkBe2010], [AkBe2009] provides the necessary generality and is beyond the classical analysis done in Sobolev spaces, due the methods employed from operator theory. We first reveal that the domain of the diffusion operator, Aα := - div α grad, depends heavily on the coefficients α where α comes from the set L ⊂ L∞. For such rough coefficients, we show that the traditional elliptic regularity fails to hold. We prove that the first order (or the mixed) formulation of Aα, Âα, provides an operator domain that is independent of α. Hence, Âα remains defined for asymptotic coefficients that are in the boundary of ∂L, i.e., α ∂L, for which Aα is ill-defined. Since a preconditioner is basically an approximate inverse, we study boundary behaviour of Aα-1 and prove its sequential continuity for α ∈ ∂L. The boundary values can be used as the dominant factor in a perturbation expansion and the preconditioned operator becomes:
Aα-1 = Aα∞-1 + O(||α - α∞ || ),
Aα∞-1 Aα∞ = I + O(||α - α∞ || ).
We provide the characterization of Aα∞-1 in [AkBe2009].

Related publications

4. Optimal multilevel preconditioning under adaptive mesh refinement

Fig. Adaptive mesh refinement.

In the case of uniform refinement, conventional multilevel preconditioners such as multigrid have optimal (O(N), where N is the number of degrees of freedom) computational and storage complexity due to the geometric increase in the size of the problem. However under adaptive mesh refinement (AMR), they become suboptimal. In 3D, we study multigrid, additive multigrid (BPX), hierarchical basis (HB), and wavelet-modified (stabilized) hierarchical basis (WHB) preconditioners [AkHo2006] and their implementation aspects under AMR [AkBoHo2003]. We give the first optimality proof of the BPX preconditioner under a realistic 3D AMR which can also be extended to arbitrary spatial dimension. Since this optimality is the fundamental assumption for the HB methods, we also give the first optimality result of the additive WHB methods [AkHo2006] with L∞ PDE coefficients for 3D and 2D AMR routines. We present further algorithmic and theoretical details in [AkBoHo2004], [AkHo2005_I], [AkHo2005_II]. We apply the multilevel preconditioners for the solution of the Poisson-Boltzmann equation with an AMR algorithm based on goal-oriented adaptivity [AkBoCyHo2012]. Our preconditioners have been implemented in the software package the Finite Element ToolKit FETK; algorithmic and implementation aspects are provided in [AkBoHo2003], [AkBoHo2004].

Related publications

5. Application areas

Our numerical methods have been used in the following application areas.

5.1 Biophysics [AkBoCyHo2012], [Ak2001], [CellBio2000]

Fig. The protein backbone of a microtubule. The electrostatic potential contours.

In the simulation of electrostatics in biomolecules [AkBoCyHo2012], [Ak2001], [CellBio2000], we solve the Poisson-Boltzmann equation utilizing our multilevel preconditioners. In particular, we utilize goal-oriented adaptivity and multilevel preconditioning [AkBoCyHo2012]. Electrostatic is used in protein ducking and folding applications, for instance, in drug design.




5.2 Computer graphics

Fig. Remeshing and texture mapping of an unstructured surface mesh.

The application of interest is in digital geometry processing [AkKhSc2005] in the form of surface mesh parametrization and remeshing of unstructured meshes. We use multilevel preconditioners to solve the Laplace-Beltrami equation and find other parametrization related weights constructing various coarse hierarchies of the finest level mesh.

5.3 Geosciences [AkGrKlSc2008], [AkKl2007], [AkKlWh2007], [AkKl2009], [AkYe2010] [AkUn2013] [AkUn2014_stokes],

We apply our preconditioners to multiphase flow problems in reservoir simulations [AkGrKlSc2008], [AkKl2007], [AkKl2009], [AkKlWh2007], [AkYe2010]]. We test the performance of our preconditioners on SPE10 (Society of Petroleum Engineering) benchmark problem. The high-contrast Stokes problem [AkUn2013], [AkUn2014_stokes] is used geodynamics to the study of earth's mantle dynamics and polymer melting in plastics industry through the process of single screw extrusion.

5.4 Numerical relativity [AkBeBoHo2008], [KoAkHoPaTi2009]

Fig. Potentials for two types of Brill waves: Holz' (left), toroidal (right) forms.

For nonlinear relativistic simulations, one needs to solve the Einstein constraints to generate initial data. In [KoAkHoPaTi2009], we propose a finite element approach for solving these equations on 3D semi-structured and multi-block grids. While the linear finite elements solution showed usual second order convergence (unacceptably low for many relativistic applications), for quadratic elements we obtain superconvergence with order 3+σ (with 0 < σ ≤ ) due to the approximate local symmetry at the mesh vertices with respect to the local inversion of the multi-block triangulations.

In [AkBeBoHo2008], we review the conformal formulation of the Einstein constraint equations, and then consider the design, analysis, and implementation of adaptive multilevel finite element-type numerical methods for the resulting coupled nonlinear elliptic system. We derive a priori and a posteriori error estimates for a broad class of Galerkin-type approximation methods based on weak formulations.

5.5 Solid mechanics [AkMe2010], [AkYe2011], [AkPa2011], [AkBeCe2017a], [AkBeCe2017b], [AkCeKi2018a]

PD is used in to model crack propagation in solid mechanics. Our numerical methods are used to solve the PD equation of motion. Furthermore, we incorporate local BCs into nonlocal theories [AkBeCe2017b], [AkCeKi2018a]. This will provide us the capability to solve important elasticity problems that require local BCs such as traction, shear, and contact.

In addition, our preconditioners are used to solve the high-contrast biharmonic plate equation [AkYe2011]. The high-contrast in material properties is ubiquitous in composite materials. Hence, the modeling of composite materials is an immediate application of the biharmonic plate equation with high-contrast coefficients.

Related publications

 

© Burak Aksoylu